
Zadanie Autobusy [B] (aut)
Pomóż nam usprawnić bazę zadań!
Autobusy [B]
Limit pamięci: 32 MB
Mały Jaś wybiera się ze swoim kolegą do muzeum. Umówili się na spotkanie przy zajezdni autobusowej. Jaś jest osobą bardzo punktualną, w związku z czym na miejsce spotkania dotarł za wcześnie. Na dworze jest zimno, dlatego Jaś postanowił czekać na swojego znajomego w autobusie. Niestety wszystkie autobusy zatrzymują się w zajezdni tylko na chwilę, zatem Jaś postanowił wsiąść do jednego z autobusów, przejechać nim pewną liczbę przystanków, a następnie przesiąść się do autobusu jadącego z powrotem do zajezdni. Ze względu na niską temperaturę, Jaś chciałby spędzić na dworze tak mało czasu, jak to tylko możliwe. W tym celu planuje zminimalizować sumaryczny czas czekania na autobus w zajezdni, czas potrzebny na przesiadkę oraz czas oczekiwania na swojego przyjaciela po powrocie do zajezdni (ze względu na swą wrodzoną punktualność, Jaś nie mógłby spóźnić się na spotkanie z kolegą). Jaś znalazł szczegółowy rozkład jazdy autobusów, który pozwoli mu zaplanować przejażdżkę. Ponieważ jednak nie jest on dobrym matematykiem, więc poprosił Ciebie o rozwiązanie swojego problemu.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia chwile przybycia Jasia i jego kolegi na miejsce spotkania oraz rozkład jazdy autobusów,
- wyznaczy najkrótszy czas, jaki Jaś musi spędzić na dworze czekając na kolegę,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu wejścia znajduje się pięć liczb całkowitych: 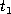 ,
, 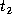 ,
, 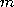 ,
,  ,
,  (
(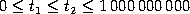 ,
,
 ,
, 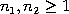 ,
, 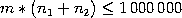 ), pooddzielanych pojedynczymi odstępami.
Liczby te
reprezentują odpowiednio: chwilę przybycia Jasia na miejsce spotkania, chwilę przybycia kolegi Jasia na miejsce spotkania,
liczbę przystanków autobusowych na trasie (wliczając w to zajezdnię), liczbę autobusów jadących z zajezdni oraz liczbę
autobusów jadących do zajezdni.
Kolejnych
), pooddzielanych pojedynczymi odstępami.
Liczby te
reprezentują odpowiednio: chwilę przybycia Jasia na miejsce spotkania, chwilę przybycia kolegi Jasia na miejsce spotkania,
liczbę przystanków autobusowych na trasie (wliczając w to zajezdnię), liczbę autobusów jadących z zajezdni oraz liczbę
autobusów jadących do zajezdni.
Kolejnych  wierszy zawiera rozkłady jazdy autobusów dla kolejnych przystanków na trasie.
Pierwszym przystankiem jest zajezdnia.
Autobusy jadące z zajezdni zatrzymują się kolejno na przystankach
wierszy zawiera rozkłady jazdy autobusów dla kolejnych przystanków na trasie.
Pierwszym przystankiem jest zajezdnia.
Autobusy jadące z zajezdni zatrzymują się kolejno na przystankach 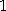 ,
, 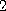 ,
,  ,
, 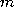 ,
natomiast autobusy wracające do zajezdni - na tych samych przystankach, ale w odwrotnej kolejności.
Każdy autobus po dojeździe do stacji pierwszej albo
,
natomiast autobusy wracające do zajezdni - na tych samych przystankach, ale w odwrotnej kolejności.
Każdy autobus po dojeździe do stacji pierwszej albo  -tej kończy kursowanie w rozważanym dniu.
Rozkład jazdy na
-tej kończy kursowanie w rozważanym dniu.
Rozkład jazdy na 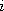 -tym przystanku składa się z
-tym przystanku składa się z 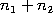 liczb całkowitych
liczb całkowitych
 , gdzie
, gdzie 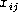 reprezentuje czas przyjazdu / odjazdu
reprezentuje czas przyjazdu / odjazdu 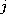 -tego autobusu.
Liczby te są pooddzielane w wierszach pojedynczymi odstępami.
Dla
-tego autobusu.
Liczby te są pooddzielane w wierszach pojedynczymi odstępami.
Dla  liczba dotyczy autobusu jadącego z zajezdni, dla
liczba dotyczy autobusu jadącego z zajezdni, dla 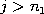 - do zajezdni.
Przybycie i odjazd każdego autobusu na każdym przystanku odbywają się w tej samej jednostce czasu.
Każdy autobus potrzebuje co najmniej jednej jednostki czasu na przejechanie pomiędzy kolejnymi przystankami
na swojej trasie.
Jaś może wsiąść do autobusu, o ile znajduje się na przystanku w momencie odjazdu tego autobusu. W szczególności, przesiadka
z autobusu A do B, jeżeli chwile ich przyjazdu na przystanek to odpowiednio
- do zajezdni.
Przybycie i odjazd każdego autobusu na każdym przystanku odbywają się w tej samej jednostce czasu.
Każdy autobus potrzebuje co najmniej jednej jednostki czasu na przejechanie pomiędzy kolejnymi przystankami
na swojej trasie.
Jaś może wsiąść do autobusu, o ile znajduje się na przystanku w momencie odjazdu tego autobusu. W szczególności, przesiadka
z autobusu A do B, jeżeli chwile ich przyjazdu na przystanek to odpowiednio  i
i 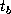 , jest możliwa, o ile
, jest możliwa, o ile  .
.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać dokładnie jedną liczbę całkowitą - najkrótszy czas, jaki Jaś musi spędzić na dworze, czekając na swojego kolegę. Jeżeli nie istnieje para autobusów, z użyciem których można wykonać opisany manewr, to należy przyjąć, że Jaś będzie cały czas oczekiwał na kolegę przy zajezdni.
Przykład
Dla danych wejściowych:0 10 3 1 2 0 9 10 3 4 8 4 3 7poprawną odpowiedzią jest:
2
W rozwiązaniu o minimalnym czasie oczekiwania Jaś wsiada na zajezdni w zerowej jednostce czasu do pierwszego autobusu, przejeżdża nim do drugiego przystanku, w czwartej jednostce czasu, wsiada w autobus powrotny o numerze dwa i dociera z powrotem do zajezdni w dziewiątej jednostce czasu.
Autor zadania: Piotr Stańczyk.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English